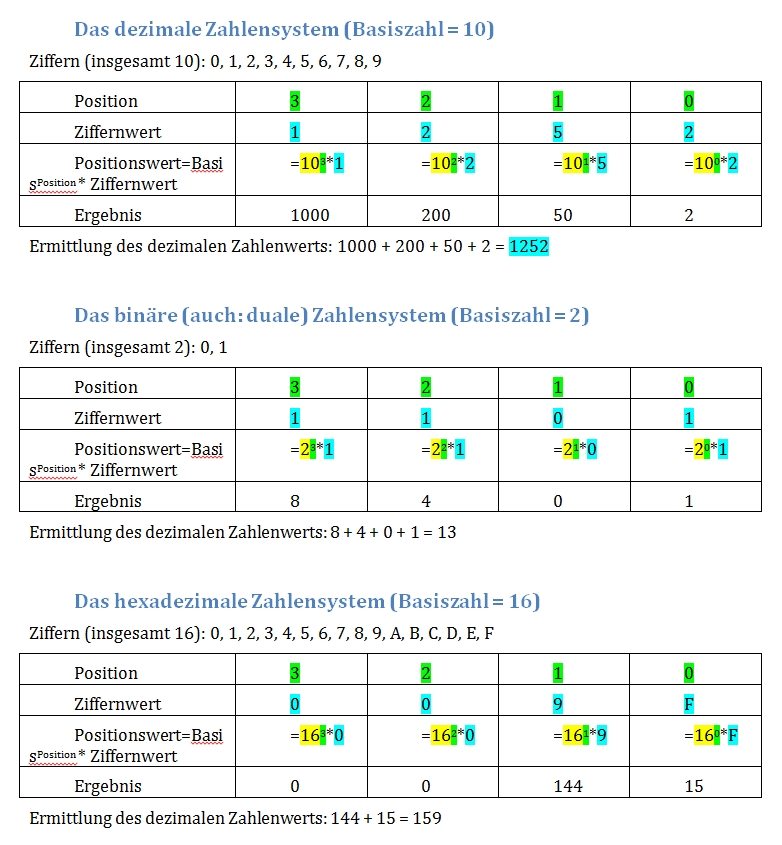
1. Stellenwertsysteme
In Stellenwertsystemen besitzt jede Stelle (Position) innerhalb einer Zahl einen festen Wert. Die Stellen werden von rechts nach links, beginnend mit der Zahl 0, durchnumeriert. Der Wert jeder einzelnen Stelle errechnet sich aus der Nummer der Stelle, indem diese als Exponent zur sog. Basiszahl des Zahlensystems erhoben wird. Die Anzahl der in einem Stellenwertsystem benötigten Ziffern entspricht grundsätzlich dem dezimalen Wert der Basiszahl: Im dezimalen Zahlensystem (Basiszahl 10) werden 10 Ziffern benötigt, nämlich die uns vertrauten von 0 bis 9. Das binäre Zahlensystem (Basiszahl 2), erfordert zwei, nämlich 0 und 1, das hexadezimale Zahlensystem (Basiszahl 16) braucht deren 16 (die Ziffern von 0 bis 9, zusätzlich werden die Buchstaben von A bis F verwendet).
Die "Beliebtheit" des hexadezimalen Zahlensystems im Bereich der Informationstechnologie erklärt sich dadurch, dass die höchste Ziffer des hexadezimalen Zahlensystems, F (= dezimal 15), genau dem maximalen Wert eines halben Bytes entspricht. Binäre Zahlen lassen sich damit vergleichsweise gut lesbar darstellen: 11000011 = C3 ; 01110011 = 73 ; 11111111 = FF

Entwurf des binären Zahlensystems von Gottfried Wilhelm Leibniz (1646-1716) aus dem Jahr 1697 (Bildquelle: <https://commons.wikimedia.org/w/index.php?title=File:Leibniz_binary_system_1697.jpg&oldid=538188681>, gemeinfrei)

Denkmal für Gottfried Wilhelm Leibniz in der Georgstraße in Hannover (https://goo.gl/maps/SjhMndAbrKwRkTRf9) (Photo: CC BY-SA Stephan Lücke 2023)
2. Additionssysteme
Neben den vorgestellten Stellenwertsystemen gibt es noch sog. Additionssysteme. Bekannteste Vertreter sind einfache Strichlisten oder auch das römische Zahlensystem. In letzterem steht die Zahl XVI für die dezimale Zahl 16, die sich aus der Additon der Ziffern X (= 10), V (= 5) und I (= 1) ergibt. In der römischen Zahl IV (= dez. 4) steht die Ziffer I wiederum für den Wert 1 - obwohl die Ziffer in diesem Fall an der zweiten Stelle von rechts steht und nicht an der ersten wie im Fall der XVI, wo sie ebenfalls für den Wert 1 steht. Im Unterschied zu den Stellenwertsystemen ändert sich der Wert einer Ziffer also nicht in Abhängigkeit ihrer Position innerhalb einer Zahl.